Line and Angles

Geometry is basically the study of different properties of point, line and plane.

• The three angles in a triangle always add up to 180⁰
• The three angles of an equilateral triangle are all equal to 60⁰
• Two angles of an isosceles triangle are equal.
• One angle of a right-angled triangle is 90⁰
• All angles of an acute-angled triangle are acute angles, thus smaller than 90⁰
• One angle of an obtuse-angled triangle is obtuse, thus larger than 90⁰ and smaller than 180⁰

Angle:

An angle is formed by two rays originating from the same end point.

The rays making an angle are called the arms of the angle and the end-points are called the vertex of the angle.

Types of Angles:-

(i) Acute angle: - An angle whose measure lies between 0° and 90°, is called an acute angle.

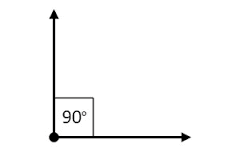
(ii) Right angle: - An angle, whose measure is equal to 90°, is called a right angle.

(iii) Obtuse angle: - An angle, whose measure lies between 90° and 180°, is called an obtuse angle.

180 degrees > Obtuse angle > 90 degrees

(iv) Straight angle: - The measure of a straight angle is 180°.

(v) Reflex angle: - An angle which is greater than 180° and less than 360°, is called the reflex angle.

(vi) Complimentary angle: - Two angles, whose sum is 90°, are called complimentary angle.

(vii) Supplementary angle: - Two angles whose sum is 180º, are called supplementary angle.

(viii) Adjacent angle: - Two angles are adjacent, if they have a common vertex, common arm and their non-common arms are on different sides of the common arm.

In the above figure angle ABC and DBC are adjacent angle. Ray BC is their common arm and point B is their common vertex. Ray BA and BD are uncommon arm.

When the two angles are adjacent, then their sum is always equal to the angle formed by the non-common arm.

Thus, angle ABD = angle ABC + angle DBC

(ix) Linear pair of angles: - If the sum of two adjacent angles is 180º, then their non-common lines are in the same straight line and two adjacent angles form a linear pair of angles.

(x) Vertically opposite angles: - When two lines AB and CD intersect at a point O, the vertically opposite angles are formed.

Angle pairs formed by parallel lines cut by a transversal

When two parallel lines are given in a figure, there are two main areas: the interior and the exterior.

When two parallel lines are cut by a third line, the third line is called the transversal. In the example below, eight angles are formed when parallel lines m and n are cut by a transversal line, t.

There are several special pairs of angles formed from this figure. Some pairs have already been reviewed:

Vertical pairs:   

• angle 1 and 4
• angle 2 and 3
• angle 5 and 8
• angle 6 and 7

Recall that all pairs of vertical angles are congruent.
 Supplementary pairs:   

• angle 1 and 2
• angle 2 and 4
• angle 3 and 4
• angle 1 and 3
• angle 5 and 6
• angle 6 and 8
• sngle 7 and 8
• angle 5 and 7

Recall that supplementary angles are angles whose angle measure adds up to 180°. All of these supplementary pairs are linear pairs. There are other supplementary pairs described in the shortcut later in this section. There are three other special pairs of angles. These pairs are congruent pairs.

Alternate interior angles 
two angles in the interior of the parallel lines, and on opposite (alternate) sides of the transversal. Alternate interior angles are non-adjacent and congruent.
 

Alternate exterior angles 
two angles in the exterior of the parallel lines, and on opposite (alternate) sides of the transversal. Alternate exterior angles are non-adjacent and congruent.
 
Corresponding angles 

two angles, one in the interior and one in the exterior, that are on the same side of the transversal. Corresponding angles are non-adjacent and congruent.